In quantum computing, a qubit is a basic unit of information used to encode quantum data. They are essentially the quantum equivalent of the traditional "bit" used in classical computers to encode information in binary form (0's and 1's). We can create qubits by manipulating quantum particles such as electrons, photons, and ions. Quantum computers use these qubits to perform advanced computations that would normally take a classical supercomputer thousands of years to complete. Here, however, I use qubits as merely a representation of quantum particles because a sufficient quantum particle dataset is not accessible.
What does a qubit look like? Imagine a two-unit sphere with a north and south pole that lie on separate points on the sphere:
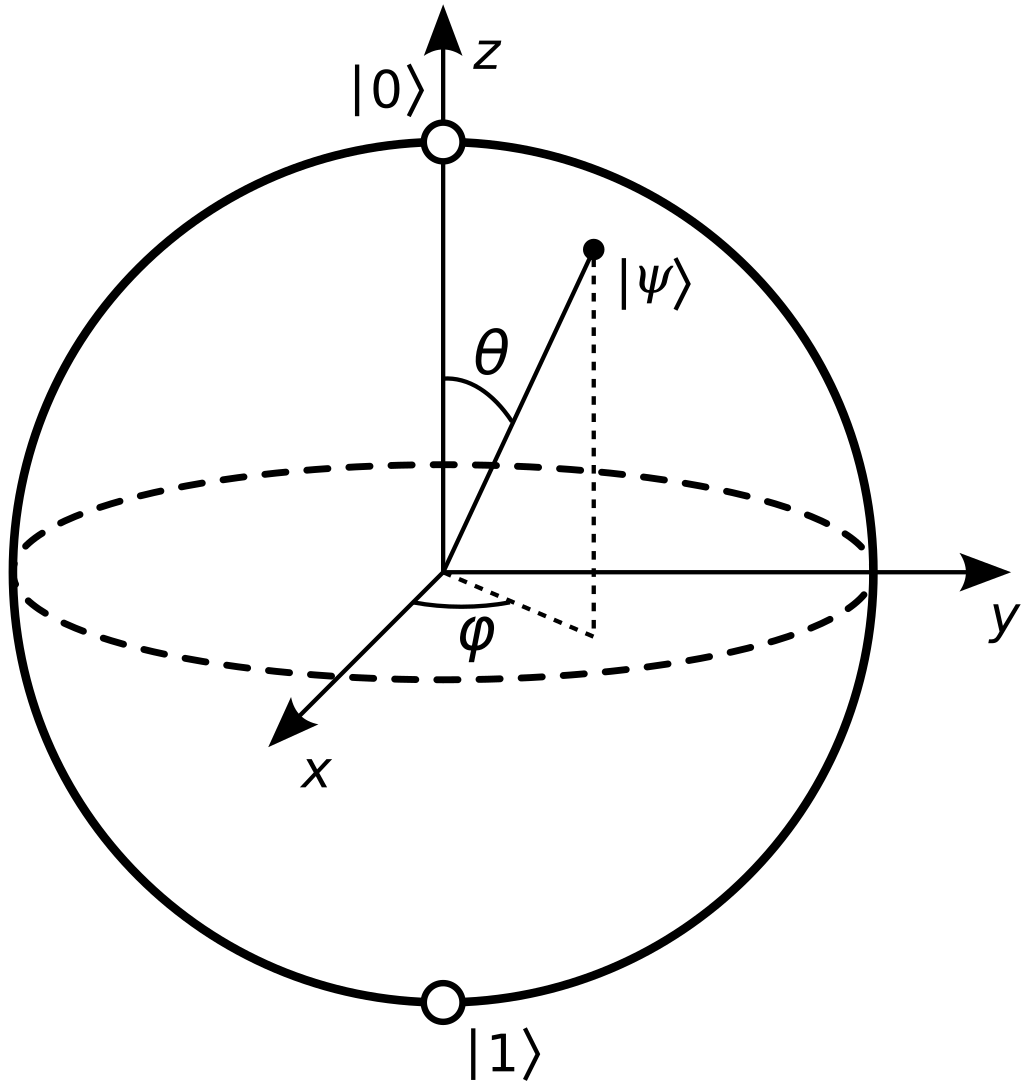
As mentioned earlier, in classical computing a bit can only represent a 0 or 1, but a qubit can exist in a state of superposition of both 0 and 1 at the same time. The "Bloch Sphere" is a visualization of this superposition, where the north pole represents the state "0", the south pole represents the state "1", and any point on the sphere corresponds to a superposition of these two states. The equator represents states with equal probability of being measured as a 0 or 1.
We will skip over most of the math for now, but a more thorough explanation can be found here.
Building The Network
The model I have adapted for this project so far is:
Where P = probability distribution of qubit states, I = initial state, and W is our weight.
This will act as the first model, but it may be beneficial to implement additional models for scalability. I could add additional quantum gates other than the Hadamard gate, or more circuit layers.